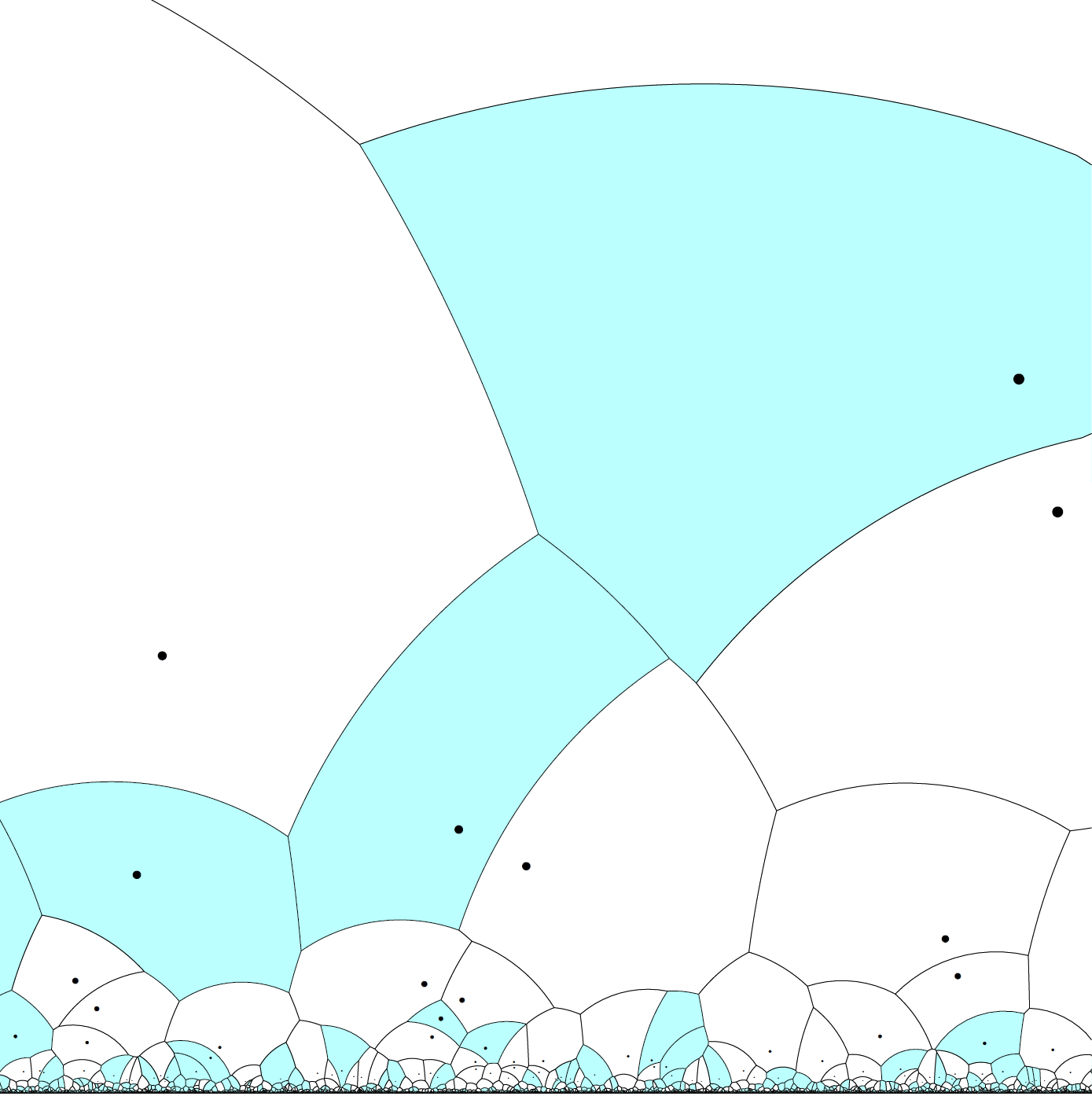
We place points as "randomly as possible" in the hyperbolic plane. Let crystal cells grow from each point until they run into another cell, we color the cells with probability $p$ and ask the question, is it possible to walk forever using only the colored cells? This formulation is quite vague. However, all else equal, if we increase $p$, then it isn't any harder to walk forever. It turns out there is a critical probability $p_c$, so that when $p> p_c,$ we have a positive probability of being able to walk forever, but if $p< p_c,$ almost surely we cannot walk forever. Imagine we have a parameter $\lambda$ that controls the average density of the points within distance one of the origin. Bollobás and Riordan showed that if we were working in the Euclidean plane, rather than the hyperbolic plane, $p_c = 1/2$ regardless of the choice of $\lambda.$ Benjamini and Schramm showed that in the hyperbolic plane $p_c$ is a function of $\lambda$ and provided some bounds. The following is joint work with my PhD supervisor Tobias Müller.

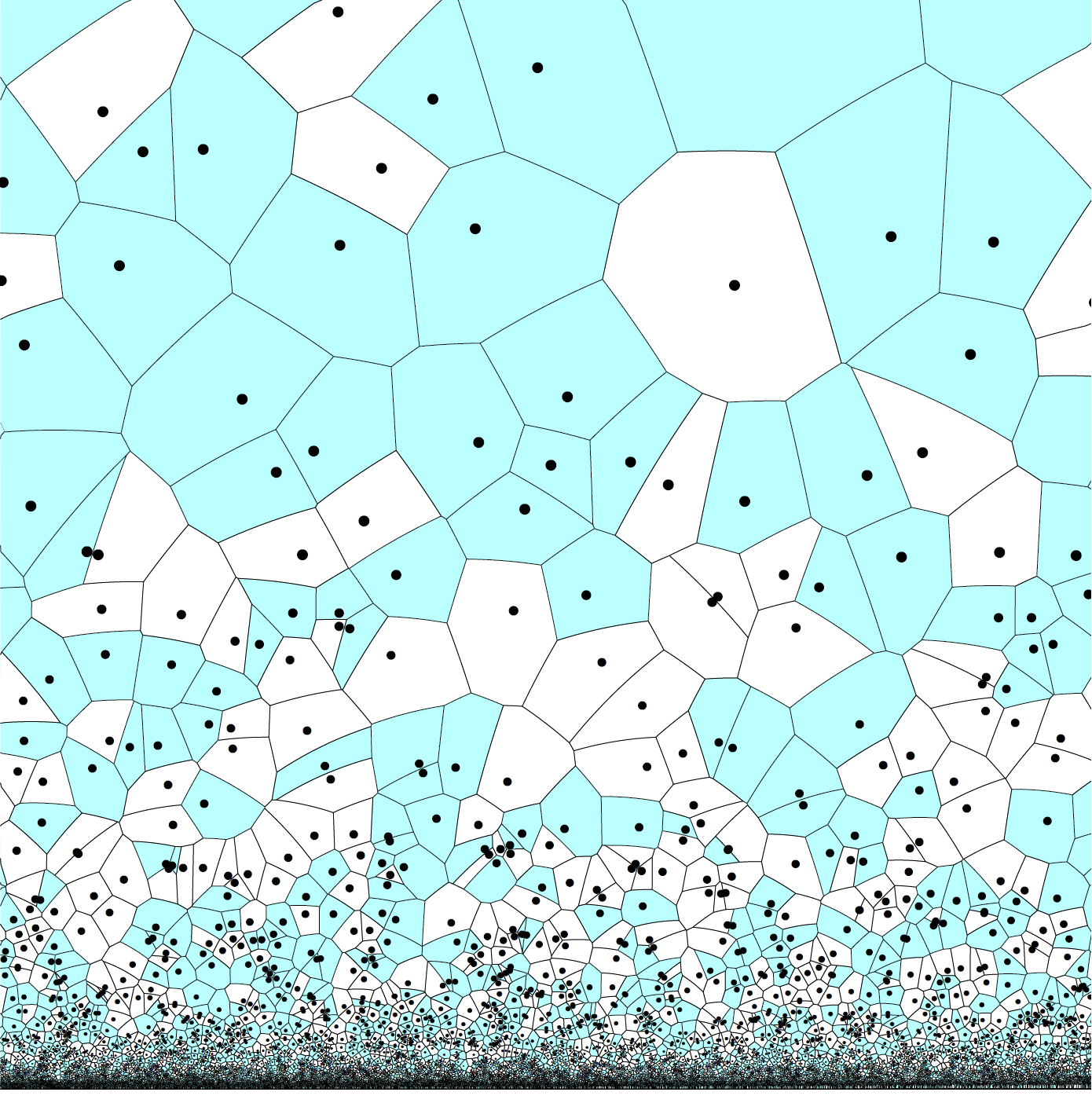
The critical probability for Voronoi percolation in the hyperbolic plane tends to $1/2$

Some intuition as to why one might expect that the large $\lambda$ limit of the critical value in the hyperbolic plane might coincide with the critical value in the Euclidean plane is given by the following observation. As we “zoom in” around any given point on the hyperbolic plane, the geometry starts to look more and more like the geometry of the Euclidean plane; and as the intensity $\lambda \to \infty$ the points of the Poisson process get packed closer and closer together. In other words, as $\lambda \to \infty$ , it becomes increasingly difficult to distinguish the “local picture” from ordinary, Euclidean Voronoi percolation. Of course the same is not necessarily true for global characteristics of the model so some other ideas are needed. This result confirms a conjecture of Benjamini and Schramm.

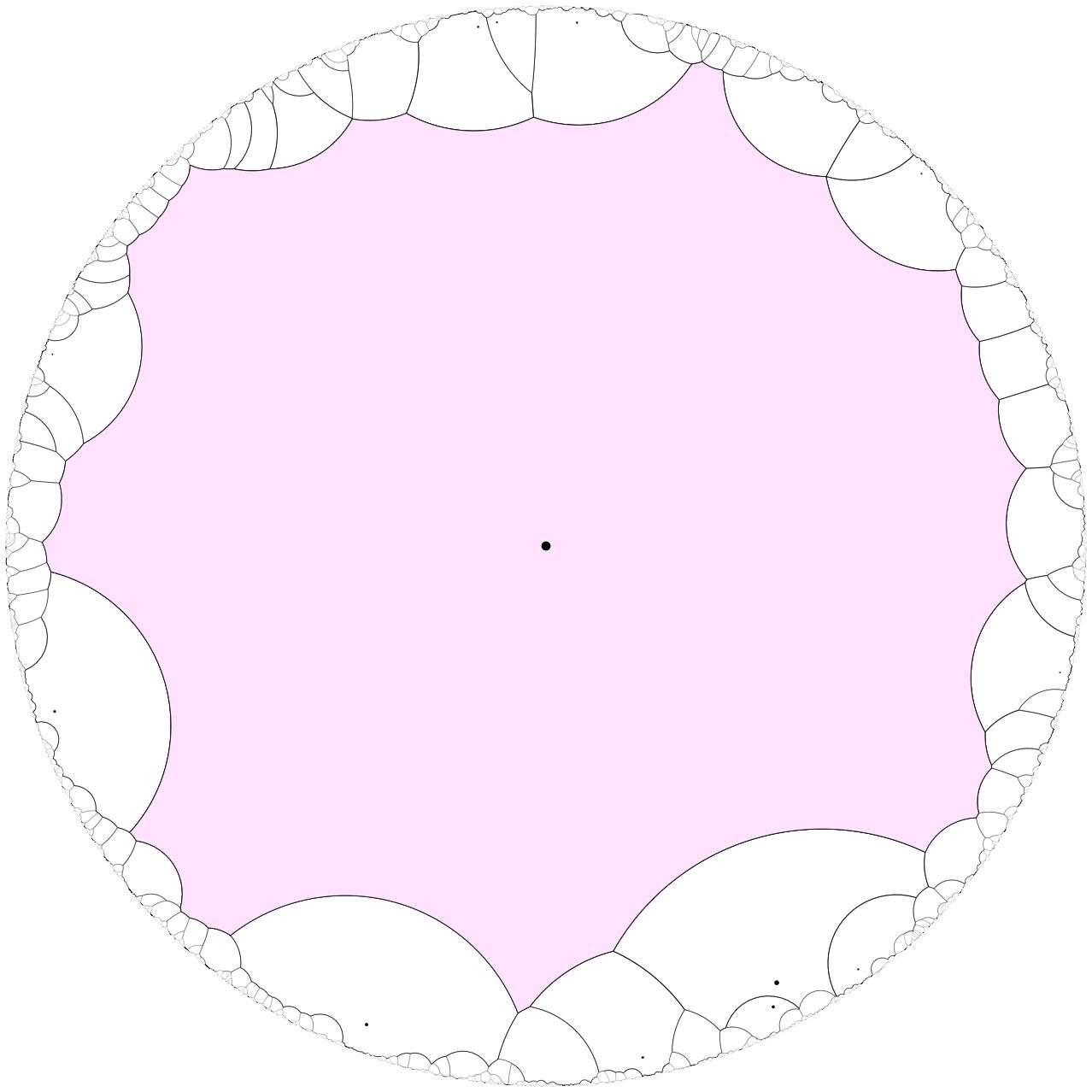
Poisson-Voronoi percolation in the hyperbolic plane with small intensities

We show that the critical probability for the existence of an infinite cluster is asymptotically equal to $\pi \lambda/3$ as $\lambda \to 0$. This answers a question of Benjamini and Schramm. The graphic shows that the number of neighbors becomes large when $\lambda$ is small.

My thesis can be viewed here. (Some of the chapters are embargoed until the contents appear in print)